原始檔案與未來教學更新資訊可於Patreon取得
您可於Twitter上追蹤我
本文屬於遊戲數學系列文
Here is the original English post
本文之英文原文在此
前備教學
大綱
內積是個簡單卻又十分有用的數學工具,它能將兩個向量的長度與方向之間的關係濃縮成一個單一數值。向量能夠應用在計算投影、反射、打光、與許多其他遊戲相關運算。
你將可透過本教學學會:
- 內積的幾何意義
- 如何將一個向量投影到另外一個向量上
- 如何沿任意軸向測量物件的尺寸
- 如何針對一個平面反射一個向量
- 如何模擬彈力球於斜坡上的行進路線
內積
假設有兩個向量,![]() 與
與![]() 。由於一個向量代表一組方向與長度的資料,其起始點位於何處都沒關係,所以就讓我們將
。由於一個向量代表一組方向與長度的資料,其起始點位於何處都沒關係,所以就讓我們將![]() 與
與![]() 的起始點重合:
的起始點重合:
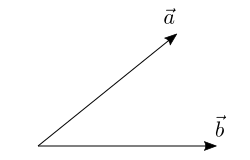
內積(dot product)是個數學運算元,它能結合兩個向量而得出一個單一數值。此值即為第一個向量投影於第二個向量上的有號長度(signed magnitude)乘以第二個向量的長度。可以把投影想成是用個平行光源將第一個向量的影子映照在第二個向量上,且光源方向與第二個向量方向垂直。
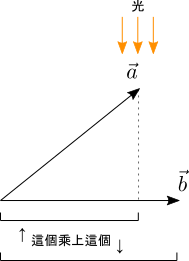
我們將![]() 與
與![]() 的內積寫成
的內積寫成![]() (念做a dot b)。
(念做a dot b)。
若兩向量之間的夾角小於90度,則第一個向量的有號長度為正(即相當於其長度)。若夾角大於90度,則第一個向量的有號長度則為負(其長度加上負號)。
兩向量何者為第一何者為第二,其實並不重要。將兩者的順序調換,內積結果仍然不變。
![]()
若![]() 是個單位向量(長度為1),則
是個單位向量(長度為1),則![]() 投影至
投影至![]() 上的有號長度便直接等於
上的有號長度便直接等於![]() .
.
內積公式 – 餘弦版
注意圖中有個直角三角形,令![]() 與
與![]() 之間的夾角為
之間的夾角為![]() :
:

記得本教學提到直角三角形的鄰邊長即為斜邊乘上角度![]() 之餘弦值,於是
之餘弦值,於是![]() 投影至
投影至![]() 上的有號長度即為
上的有號長度即為![]() :
:

兩項量的內積可以表達成兩項量各自的長度與夾角之餘弦值三者相乘,本算式同時也驗證了內積之兩項量前後順序並不影響結果的特性:
![]()
若兩項量![]() 與
與![]() 皆為單位向量,則
皆為單位向量,則![]() 即等於
即等於![]() .
.
若兩向量互相垂直(夾角90度),則內積值為零。若夾角小於90度,則內積值為正。若夾角大於90度,則內積值為負。由此可見,利用兩項量之內積的正負號,便已可粗略知道兩者方向的同異性。
由於![]() 單向性地減少直至
單向性地減少直至![]() ,兩向項量的方向越相近,兩者之內積值便越大;而兩項量的方向越相反,則兩者之內積值越小。當兩項量的方向完全一樣或恰恰相反,則兩者之內積值分別為
,兩向項量的方向越相近,兩者之內積值便越大;而兩項量的方向越相反,則兩者之內積值越小。當兩項量的方向完全一樣或恰恰相反,則兩者之內積值分別為![]() 和
和![]() 。
。
內積公式 – 分量版
當我們以三個分量組成一個3D向量的方式表達兩個3D向量時(總共六個浮點數),兩個向量之夾角並不是馬上就看得出來的。幸好有另外一個不需要用到夾角餘弦的內積計算方式,假設![]() 與
與![]() 的分量為:
的分量為:
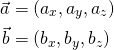
那麼兩項量之內積值即等於三個軸向的分量各自相乘之後再相加:
![]()
不但簡單,又不需要用到餘弦函數!
Unity提供Vector3.Dot函式,以計算兩個向量之內積:
float dotProduct = Vector3.Dot(a, b);
以下為該函式的一種實作:
Vector3 Dot(Vector3 a, Vector b)
{
return a.x * b.x + a.y * b.y + a.z * b.z;
}
計算向量長度的算式為![]() ,可用向量與自身的內積來表達:
,可用向量與自身的內積來表達:
![]()
記得先前得出的內積算式![]() 。這表示若兩向量的內積與長度已知,我們便可用反餘弦函數算出兩向量之間的夾角:
。這表示若兩向量的內積與長度已知,我們便可用反餘弦函數算出兩向量之間的夾角:
![]()
若![]() 與
與![]() 皆為單位向量,則省略向量長度的計算後可以更進一步簡化上述算式:
皆為單位向量,則省略向量長度的計算後可以更進一步簡化上述算式:
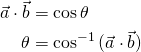
向量投影
我們已知向量內積的幾何定義,即為一被投影向量之有號長度與另一向量之長度相乘。現在就讓我們來看看如何將一個向量投影到另外一個向量上。令![]() 表示
表示![]() 投影至
投影至![]() 上的結果:
上的結果:
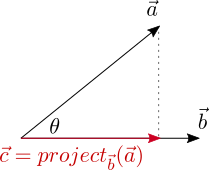
與![]() 方向相同的單位向量為
方向相同的單位向量為![]() ,所以若我們將其乘上
,所以若我們將其乘上![]() 投影到
投影到![]() 上的有號長度,便可得到
上的有號長度,便可得到![]() 。換句話說,
。換句話說,![]() 與
與![]() 方向平行,且其長度等於
方向平行,且其長度等於![]() 投影至
投影至![]() 上的長度。
上的長度。
既然內積![]() 為
為![]() 的長度乘上
的長度乘上![]() 投影至
投影至![]() 上的有號長度,
上的有號長度,![]() 的有號長度就是
的有號長度就是![]() 與
與![]() 的內積除以
的內積除以![]() 的長度:
的長度:
![]()
將此有號長度乘上單位向量![]() 便可得到向量投影的算式:
便可得到向量投影的算式:
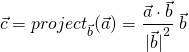
由於![]() ,投影算式也可寫成:
,投影算式也可寫成:
![]()
若![]() 為單位向量,則更可進一步簡化投影算式:
為單位向量,則更可進一步簡化投影算式:
![]()
Unity提供Vector3.Project函式,以計算將一個向量投影至另一向量上:
Vector3 projection = Vector3.Project(vec, onto);
以下為該函式的一種實作:
Vector3 Project(Vector3 vec, Vector3 onto)
{
float numerator = Vector3.Dot(vec, onto);
float denominator = Vector3.Dot(onto, onto);
return (numerator / denominator) * onto;
}
有時候需要留意一個退化狀況,也就是作為投影目標的向量本身長度為零或近乎零,如此便會造成除以零的運算而導致數值爆炸。單單只用Unity的Vector3.Project函式即有可能會遇到此狀況。
處理此狀況的方法之一,是預先運算作為投影目標的向量長度。若長度太小,則改用另外一個長度夠大的後備向量作為投影目標(如+X單位向量、角色正前方向量等):
Vector3 SafeProject(Vector3 vec, Vector3 onto, Vector3 fallback)
{
float sqrMag = v.sqrMagnitude;
if (sqrMag > Epsilon) // 與一個極小數相比
return Vector3.Project(vec, onto);
else
return Vector3.Project(vec, fallback);
}
習題:量尺
現在來看個向量投影的習題:製作一個任意軸向的量尺,以測量物件延此軸向的尺寸。
我們用個基準點(base)和軸向(axis)代表量尺:
struct Ruler
{
Vector3 Base;
Vector3 Axis;
}
欲將一個點投影到量尺上,首先,找出該點對於量尺基準點的相對向量。接下來,將此向量投影至量尺軸向上。最後,將量尺基準點沿著量尺軸向以此向量投影位移,即可得該點於量尺上之投影:
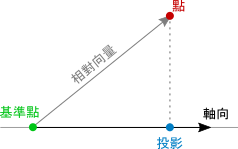
Vector3 Project(Vector3 vec, Ruler ruler)
{
// 計算相對向量
Vector3 relative = vec - ruler.Base;
// 投影
float relativeDot = Vector3.Dot(vec, ruler.Axis);
Vector3 projectedRelative = relativeDot * ruler.Axis;
// 從基準點位移
Vector3 result = ruler.Base+ projectedRelative;
return result;
}
名為relativeDot的中介值,基本上即為點之投影與量尺基準點沿著量尺軸向之有號距離,若與軸向相同則為正,若與軸向相反則為負。
計算物件模型中的每一個頂點投影到量尺上的有號距離,取得最小與最大的有號距離,最大值減最小值即為該物件沿著量尺軸向測量出的尺寸。從量尺基準點,位移量尺軸向乘以最小與最大之有號距離,則可得到該物件投影到量尺上的兩個端點。
void Measure
(
Mesh mesh,
Ruler ruler,
out float dimension,
out Vector3 minPoint,
out Vector3 maxPoint
)
{
float min = float.MaxValue;
float max = float.MinValue;
foreach (Vector3 vert in mesh.vertices)
{
Vector3 relative = vert- ruler.Base;
float relativeDot = Vector3.Dot(relative , ruler.Axis);
min = Mathf.Min(min, relativeDot);
max = Mathf.Max(max, relativeDot);
}
dimension = max - min;
minPoint = ruler.Base+ min * ruler.Axis;
maxPoint = ruler.Base+ max * ruler.Axis;
}
向量反射
接著我們要來看如何計算向量![]() 針對法向量為
針對法向量為![]() 之平面的反射:
之平面的反射:
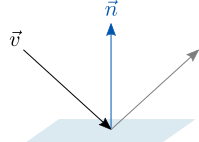
我們可將向量拆解成與平面平行的分量![]() 和與平面垂直的分量
和與平面垂直的分量![]() :
:
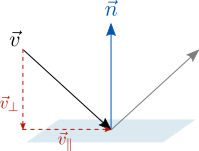
![]()
垂直分量便是向量投影至平面法向量上的結果,而平行分量則是原本向量減去垂直分量:
![]()
將平行分量方向反轉再加上垂直分量,便可得到向量對平面反射的結果。

令反射為![]() ):
):
![]()
若我們將![]() 以
以![]() 代入,則可得到另一種向量反射算式:
代入,則可得到另一種向量反射算式:
![]()
Unity提供Vector3.Reflect函式,以計算向量反射:
float reflection = Vector3.Reflect(vec, normal);
以下為該函式的一種實作:
Vector3 Reflect(Vector vec, Vector normal)
{
Vector3 perpendicular= Vector3.Project(vec, normal);
Vector3 parallel = vec - perpendicular;
return parallel - perpendicular;
}
而以下為使用另一種向量反射算式之實作:
Vector3 Reflect(Vector vec, Vector normal)
{
return vec - 2.0f * Vector3.Project(vec, normal);
}
習題:彈力球與斜坡
現在我們知道如何反射向量,我們便已具備足夠知識,以模擬彈力球於斜坡上的行進路線:
我們將使用於先前的教學中所提到的尤拉方法(Euler Method)來模擬受重力影響的球之行進路線:
ballVelocity+= gravity * deltaTime; ballCenter += ballVelocity* deltaTime;
欲偵測球與斜坡的碰撞,我們必須知道如何偵測一個球體是否以穿透了一個平面。
球體可用球心與半徑代表,平面可用法向量與平面上之一點代表。令球心為![]() 、球半徑為
、球半徑為![]() 、平面法向量為
、平面法向量為![]() (單位向量)、平面上一點為
(單位向量)、平面上一點為![]() 。並且,令從
。並且,令從![]() 至
至![]() 的向量為
的向量為![]() 。
。
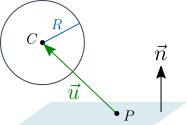
若球體沒有穿透平面,與平面垂直的![]() 分量(標記為
分量(標記為![]() )應該與為同個方向
)應該與為同個方向![]() ,且其長度不小於
,且其長度不小於![]() 。
。
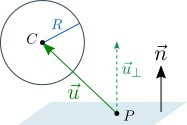
換句話說,若![]() ,則表示球體沒有穿透明面。否則,球體便以穿透平面,且穿透量為
,則表示球體沒有穿透明面。否則,球體便以穿透平面,且穿透量為![]() ,這個時候便需要修正球心位置。
,這個時候便需要修正球心位置。
欲修正球心位置,我們只需要將球體沿著平面法向量![]() 的方向移動穿透量。這個作法是個簡單的近似,並非物理正確的做法,但已足夠應付本習題。
的方向移動穿透量。這個作法是個簡單的近似,並非物理正確的做法,但已足夠應付本習題。
// 若無穿透,回傳原始球心位置
// 若有穿透,回傳修正後之球心位置
void SphereVsPlane
(
Vector3 c, // 球心位置
float r, // 球半徑
Vector3 n, // 平面法向量(單位向量)
Vector3 p, // 平面上一點
out Vector3 cNew, // 球心位置輸出
)
{
// 原始球心位置為預設值
cNew = c;
Vector3 u = c - p;
float d = Vector3.Dot(u, n);
float penetration = r - d;
// 有無穿透?
if (penetration > 0.0f)
{
cNew = c + penetration * n;
}
}
將球心修正邏輯安排到積分邏輯後面:
ballVelocity += gravity * deltaTime; ballCenter += ballVelocity* deltaTime; Vector3 newSpherePosition; SphereVsPlane ( ballCenter, ballRadius, planeNormal, pointOnPlane, out newBallPosition ); ballPosition = newBallPosition;
球穿透斜面後的位置修正,伴隨著速度向量對著斜面反射,便可模擬球從斜面反彈的效果。
上面的動畫展示的是完全彈性碰撞,且看起來不自然。正常來說,反彈力道會隨著反彈次數因能量消耗而減少,於是球會越彈越低。
一般來說,會用一個單一彈性值(restitution)來模擬兩物件之間的碰撞。當彈性為100%,則球會完美反彈。當彈性為50%,則球平行於斜面法向量的速度分量會於反彈後減半。彈性即為球平行於斜面法向量的速度分量於碰撞後與碰撞前之比例。以下為將彈性納入考量的向量反射函數:
Vector3 Reflect
(
Vector3 vec,
Vector3 normal,
float restitution
)
{
Vector3 perpendicular= Vector3.Project(vec, normal);
Vector3 parallel = vec - perpendicular;
return parallel - restitution * perpendicular;
}
此為將彈性納入考量而修改的SphereVsPlane函數:
// 若無穿透,回傳原始球心位置
// 若有穿透,回傳修正後之球心位置
void SphereVsPlane
(
Vector3 c, // 球心位置
float r, // 球半徑
Vector3 v, // 球速度
Vector3 n, // 平面法向量(單位向量)
Vector3 p, // 平面上一點
float e, // 彈性
out Vector3 cNew, // 球心位置輸出
out Vector3 vNew // 球速度輸出
)
{
// 原始球心位置與球速度為預設值
cNew = c;
vNew = v;
Vector3 u = c - p;
float d = Vector3.Dot(u, n);
float penetration = r - d;
// 有無穿透?
if (penetration > 0.0f)
{
cNew = c + penetration * n;
vNew = Reflect(v, n, e);
}
}
然後將球心位置修正邏輯用完整的反彈邏輯取代:
ballVelocity+= gravity * deltaTime; spherePosition += ballVelocity* deltaTime; Vector3 newSpherePosition; Vector3 newSphereVelocity; SphereVsPlane ( spherePosition , ballRadius, ballVelocity, planeNormal, pointOnPlane, restitution, out newBallPosition, out newBallVelocity; ); ballPosition= newBallPosition; ballVelocity= newBallVelocity;
現在,我們終於能模擬不同彈性的彈力球於斜坡上的行進路線:
總結
透過本教學,我們認識了向量內積的幾何意義,以及其算式(餘弦版本與分量版本)。
另外,我們瞭解了如何用內積計算向量投影,和如何用向量投影測量物件沿任意量尺軸向之尺寸。
最後,我們學會了用內積反射向量,及如何用項量反射模擬彈力球於斜坡上的行進路徑。
若您喜歡這篇教學,請考慮到Patreon支持我。感謝!

