遊戲數學：反三角函數、斜坡角度、與物件面向

原始檔案與未來教學更新資訊可於Patreon取得
您可於Twitter上追蹤我

本文屬於遊戲數學系列文

Here is the original English post
本文之英文原文在此

前備教學

• 三角函數基礎 – 正弦與餘弦
• 三角函數基礎 – 正切、三角形、與砲彈

大綱

我們已經認識了三個基礎三角函數：正弦、餘弦、與正切。現在我們要來看看它們的反函數、以及如何將其利用於遊戲開發。

你將可透過本教學學會：

• 三個基礎三角函數的反函數
• 如何從給定的斜率算出斜坡的角度

• 反三角函數的定義域與值域
• 特殊的方便反三角函數atan2
• 如何使物件面相滑鼠游標

反函數

一個函數能被視為一個黑盒子，能夠將給定的輸入值轉換成特定的輸出值。若一個函數能將輸入值轉換為輸出值，我們便將其寫成 (唸做y equals f of x)。若一個函數能將的輸出值當作輸入值，而給出的原始輸入值作為輸出值，我們便稱該函數為的反函數，寫成 (唸做 f inverse)。

換句話說，若對一個函數輸入而得到 (寫作)，那麼便可對反函數輸入而得到 (寫作)。

舉例來說，一個將輸入值加一的函數，其反函數為一個將輸入值減一的函數。讓我們將前者寫成，然後後者寫成。若我們將輸入到，便可算得：

   

當我們把的輸出值反輸入到，我們則可得到一開始的：

   

反三角函數

我們已經知道三角函數的輸入值是角的大小，然後其輸出值是個實數。若將三角函數的輸出值作為輸入值餵入它們的反函數，反函數將會輸出原本三角函數輸入的角(單位為弳度)。舉例來說，已知，於是可得。

反三角函數有特殊的名字。 (反正弦)不是唸做sine inverse，而是唸做arcsine。同樣地，(反餘弦)和(反正切)分別唸做arccosine和arctangent。於Unity中，呼叫反三角函數的方式如下：

float sinAngle = Mathf.Asin(sinValue); // arcsine
float cosAngle = Mathf.Acos(cosValue); // arccosine
float tanAngle = Mathf.Atan(tanValue); // arctangent

斜坡角度

現在來看個簡單的範例。給定遊戲場景中一斜坡的垂直變量和水平變量，要如何算出斜坡的角度？畫成以下的示意圖，又如何從垂直變量和水平變量算出角度？

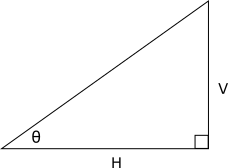
目標是用和表達。首先，我們可用正切函數寫出與和之間的關係：

   

接著，我們便可藉由將輸入來取得：

   

從另一個角度來看，上述等式可以看成是更之前的等式兩邊值各輸入反正切函數的結果。一般來說，會相消成，而則會相消成。

的單位為弳度。如同先前的教學所提到，可以將其乘上以把單位轉換為角度。

於是，現在我們可以做個簡單的互動程式，讓使用者移動一個點，該點與原點形成一個斜坡，並且用該點的座標計算斜坡的角度。

這是程式碼：

Vector3 point = p.transform.position;

// compute slope angle in radians
float angleRad = Mathf.Atan(point.y / point.x);

// convert to degrees
// Mathf.Rad2Deg is a constant equal to 180.0f / Pi
float angleDeg = angleRad* Mathf.Rad2Deg;

text = angleDeg + "°";

定義域與值域

使用反三角函數時，了解其定義域(domain)與值域(range)是非常重要的。

一個函數的定義域是所有有效輸入值的集合，而其值域則為所有可能的輸出值的集合。

舉例來說，的定義域為所有實數，因為任何角度都能作為其輸入值。而的值域則為，這個表示式代表涵蓋介於-1和1之間所有值的集合，並包含邊界值-1與1。若該表示式使用的是小括弧而非中括胡，則表示邊界值不包含在該集合內。例如表示涵蓋介於0與10之間所有值的集合，並包含邊界值0，但不包含邊界值10。

反函數的定義域與值域分別就是其對應函數的值域和定義域吧？對反三角函數來說，事實並非如此。

三角函數是週期函數，這表示不同的輸入值可以對應到同一個輸出值。對正弦函數與餘弦函數來說，甚至同一個週期內的不同輸入值也有可能對應到同一個輸出值。

讓我們再用作為範例，與的輸出值都是1，所以的輸出值是什麼？輸出值不可能同時等於、、或任何能夠讓輸出1的輸入值。事實上，反三角函數值域已被選定為特定的公認有限範圍。

與的值域皆為，所以與的定義域皆為。與的值域則分別被選定為與，這些值域涵蓋弳(或180度)的角範圍。

所以的輸出值為，這是於範圍內，唯一能輸入並得到1的角度。

接著來看，由於的值域為所有實數的集合，的定義域即為所有實數的集合。而的值域則被選定為，與的值域相同。

方便的Atan2函式

假設於2D平面上有個點且其位於第一象限內，意即且 。另外，令為介於軸與連接原點與的線段之間的角。

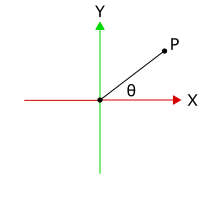
我們知道所以我們可以用反正切函數和的座標算出：。因為和皆為正數，便會位於範圍內，也同時被包含在較大的反正切函數的值域之中.

上述計算的程式碼如下：

float angle = Mathf.Atan(p.y / p.x);

那麼如果位於第四象限，意即和 ，又會如何？成為負數，而則會輸出個負角，位於範圍內，也同時被包含在較大的反正切函數的值域之中。

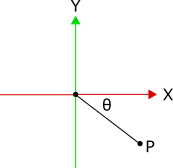
但當位於第二或第三象限的時候，問題就來了。若位於第二象限，也就是且，比例便是負的。於第二象限中，我們能夠找到一個點使得比例值相等於第四象限一點的座標比例。符合此條件的點配對滿足等式。

下圖中的兩點與有著相同的座標比例。

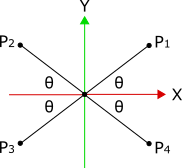
於上圖中，可以看到第一象限中的點與第三象限中的點，它們的座標比例與和的座標比例只差在正負號。所有介於連接原點與各點的線段與X軸所夾之絕對銳角(小於90度之角)都相等。

座標比例值等同於 ，也等同於。所以，若我們將傳入反正切函數，其輸出值相會等同於之輸出值，因為位於第四象限的角位於反正切函數的值域內，而位於第二象限的角則在值域外。

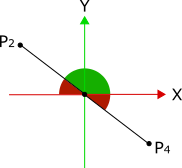
當我們將輸入反正切函數時，我們真正想要得到的是下圖中的綠色正頓角(大於90度的角)，而非紅色的負銳角。算角度的時候，一般都是從+X方向開始計算。

欲達此目的，我們須將在合併與成為單一比例值傳入反正切函數以前，檢查與 各自的正負號。然後，若角並非位於反正切函數的值域內，我們便修正反正切函數的輸出值，使其位於正確的象限內。以下是如此修正角度的程式碼：

// range of this function is (-pi, pi]
float FixedUpAtan(float py, float px)
{
  if (px > 0.0f) // normal, no fix-up needed
  {
    // "normal"
    // py > 0.0f : first quadrant
    // py < 0.0f : fourth quadrant
    return Mathf.Atan(py / px);
  }
  else if (px < 0.0f) // fix-up needed
  {
    if (py > 0.0f) // second quadrant
      return Math.PI + Mathf.Atan(py / px);
    else if (py < 0.0f) // third quadrant
      return -Math.PI + Mathf.Atan(py / px);
    else // angle on negative X axis
      return 2.0f * Mathf.PI;
  }
  else // infinity
  {
    if (py > 0.0f)
      return 0.5f * Mathf.PI; // ratio is positive infinity
    else if (py < 0.0f)
      return -0.5f * Mathf.PI; // ratio is negative infinity
    else
      return 0.0f; // degenerate input (the origin)
  }
}

這程式碼看起來有點分量，不過幸運的是，幾乎任何程式語言的標準數學函示庫內都已經有個方便的atan2函數，其值域涵蓋完整的360度，且該函數就是在做上述的角度修正(並且幾乎肯定是用更加有效率且優化的方式計算)。注意上述程式碼中，傳入的參數順序為Y先X後，不同函式庫的atan2函數參數順序可能有所不同，不過就我所看過的大部分都是Y先X後。

我常常看到一個對atan2函數的誤解，說它只是反正切函數的另外一個替代方案，與正切函數提供的功能沒有差異，這其實是錯的。反正切函數只接受單一輸入值，並且其值域為只涵蓋180度的。而atan2函數接收兩個輸入值(與在被結合為單一比例值之前)，並且其值域涵蓋了完整的360度。

使物件於3D空間中面相滑鼠游標

最後，讓我們來看看一個經典範例：使物件面向滑鼠游標。

首先，找出滑鼠游標下的射線(ray)與代表地面的平面(plane)之交點。然後，將一個物件定位於該交點，做出該物件於3D空間中跟著滑鼠游標移動的效果。這個物件就是我們的面相目標。

Camera cam = Camera.current;
Vector3 mouse= Input.mousePosition;
Ray ray = cam.ScreenPointToRay(mouse);
float rayDist;
plane.Raycast(ray, out rayDist);
sphere.position = ray.GetPoint(rayDist);

接下來，讓我們再度使用彈彈特效工具包中的熟面孔：幽浮兔。當沒有被套用任何旋轉的時候，她的正面是+X方向，而她的左邊則是+Z方向。最終目標是要讓她的正面面向目標。

以幽浮兔為原點，計算面向目標相對於她的座標：

Vector3 coord = 
  sphere.transform.position 
  - ufoBunny.transform.position;

現在來將X軸與連接幽浮兔和面向目標的線段之間的角度標記為：

我們之前已經看過，在這情況下要如何計算了，使用方便的atan2函數：

float thetaRad = Mathf.atan2(coord.z, coord.x); // in radians

現在回顧一下這張圖：

圖中的是XY平面，隨著值增加，便會逆時針繞著原點旋轉。這個旋轉軸為+Z軸(之後的教學會有更詳細的解釋)。幽浮兔與面向目標位於XZ平面上，要將XY平面的計算轉換到XZ平面上，我們需要將+X軸對應到+X軸，+Y軸對應到+Z軸，而作為旋轉軸的+Z軸則對應到-Y軸。

現在我們有了旋轉軸與旋轉角度，我們終於可以建構代表該旋轉的四元數(quaternion)。未來將會有專門介紹四元數的教學，當下我們只需要知道四元數是Unity用來表示物件旋轉的資料格式。

float thetaDeg = thetaRad * Mathf.Rad2Deg; // in degrees
float axis = Vector3.down; // (0, -1, 0) == -Y axis
Quaternion rot = Quaternion.AngleAxis(thetaDeg, axis);
ufoBunny.transform.rotation = rot;

這是最終結果：

註：Unity本身已提供如Quaternion.LookRotation與Transform.LookAt等輔助函式，能用來達到相同的效果。不過，本教學的目的在於幫助理解反三角函數。

總結

透過本教學，我們認識了反三角函數、它們與其相對應的三角函數之間的關係、以及它們的定義域與值域。

另外，我們知道了反正切函數的值域並沒有涵蓋完整的360度範圍，而atan2此方便函數的值域則有涵蓋360度範圍。

最後，我們學會了如何使用atan2函數製作經典的使物件面相滑鼠游標的效果。

若您喜歡這篇教學，請考慮到Patreon支持我。感謝！